Last Thursday I watched Wolfgang Viechtbauer’s stream
on Twitch. Wolfgang spoke about linear regression.
(If you’re interested in the results: Wolfgang lists the R-code he wrote during
the stream at https://www.wvbauer.com/doku.php/live_streams.)
During the stream we had an example with one categorical and one numeric predictor
and we built a model with interaction between these two predictors.
So the result is a straight line for each value of the categorival group.
The question was if it makes a difference if you build a simple linear model for
each group.
So let’s look at it.
Example
Let’s start and build some sample data:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
options(tidyverse.quiet = TRUE)
library(tidyverse)
parameters <- tribble(
~class_name, ~intercept, ~slope, ~sd,
"A", 5, 0.5, 5,
"B", 6, -0.5, 5,
"C", 7, 1, 5,
)
generate_class <- function(n, class_name, intercept, slope, sd) {
start <- 0
end <- 10
values <- tibble(
class_name = rep(class_name, times = n),
x = runif(n, start, end),
y = intercept + x * slope + rnorm(n, sd)
)
return(values)
}
set.seed(42)
data <- pmap_dfr(parameters %>% mutate(n = 20), generate_class)
|
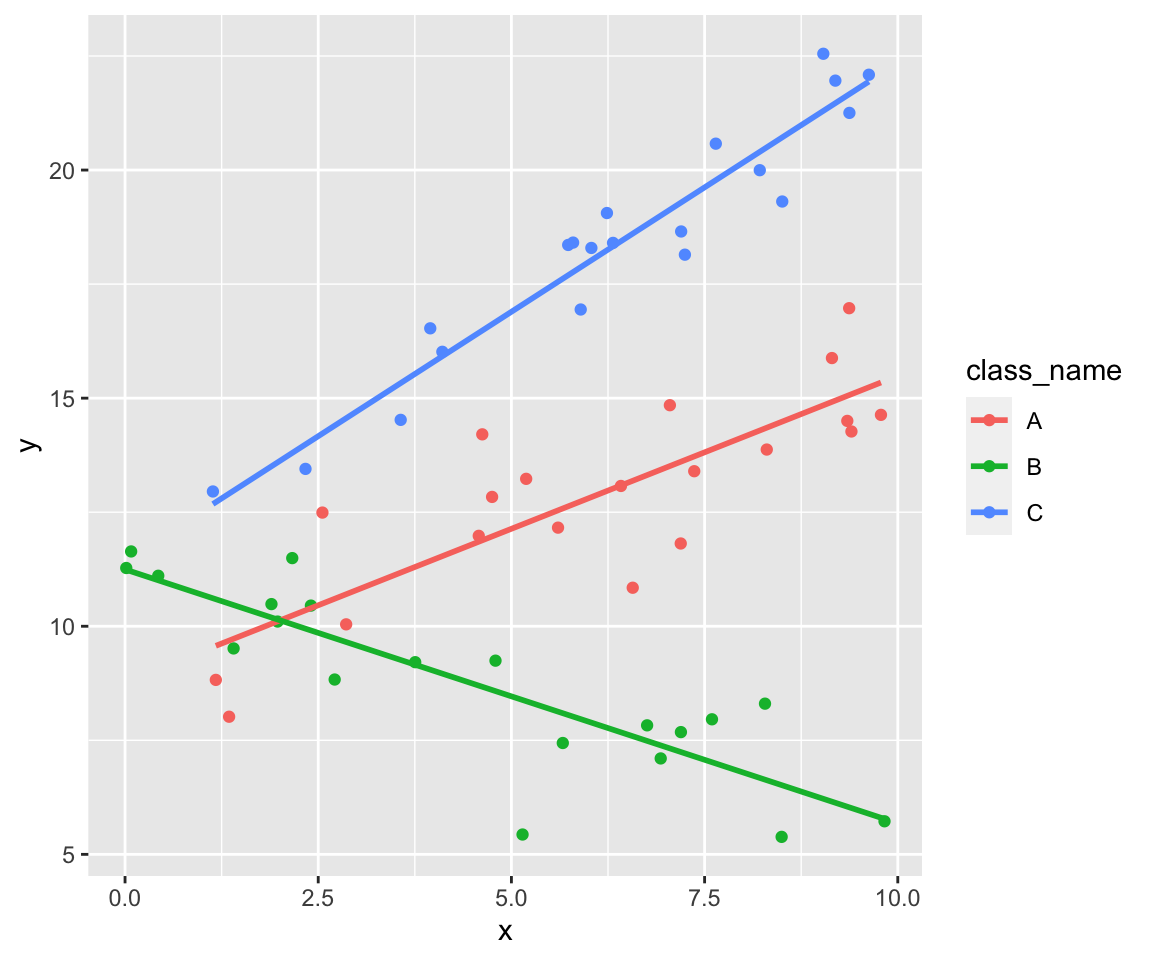
So we get three clouds of points. Each cloud follows its own line.
1
2
3
4
|
data %>%
ggplot(aes(x, y, color = class_name)) +
geom_point() +
stat_smooth(formula = y ~ x, method = lm, se = FALSE)
|
Build one linear model
We’re building the model without an intercept by using 0 + as start of the
formula so we get the intercept for each group directly (without building the
sum of the reference group and the other groups.)
1
2
|
model_complete <- lm(y ~ 0 + class_name + class_name:x, data = data)
summary(model_complete)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
##
## Call:
## lm(formula = y ~ 0 + class_name + class_name:x, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.94880 -0.65484 0.06566 0.66447 2.32326
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## class_nameA 8.78346 0.60220 14.586 < 2e-16 ***
## class_nameB 11.24628 0.42291 26.592 < 2e-16 ***
## class_nameC 11.43872 0.69364 16.491 < 2e-16 ***
## class_nameA:x 0.67056 0.09012 7.441 7.93e-10 ***
## class_nameB:x -0.55649 0.07967 -6.985 4.35e-09 ***
## class_nameC:x 1.09090 0.10240 10.653 6.95e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.071 on 54 degrees of freedom
## Multiple R-squared: 0.9948, Adjusted R-squared: 0.9942
## F-statistic: 1727 on 6 and 54 DF, p-value: < 2.2e-16
|
Build three different models
Now build a linear model for each group.
1
2
3
4
5
|
model_split <- data %>%
group_by(class_name) %>%
group_map(~ coef(summary(lm(y ~ x, data = .x))))
model_split
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.7834572 0.7482108 11.739282 7.181449e-10
## x 0.6705587 0.1119703 5.988718 1.153349e-05
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.2462761 0.40929811 27.476980 3.773904e-16
## x -0.5564857 0.07710095 -7.217624 1.027562e-06
##
## [[3]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.438716 0.5000135 22.87681 9.354783e-15
## x 1.090904 0.0738192 14.77805 1.653770e-11
|
Comparison
As you can see the coefficients are the same but the standard error of the
coefficients are different.
“What’s the reason?” I was asking myself.
Simple example
So I began to look at a simpler example:
1
2
3
4
5
6
7
8
9
10
11
|
data <- tribble(
~class_name, ~x, ~y,
"A", 0, 1,
"A", 10, 11,
"A", 10, 21,
"B", 0, 0,
"B", 10, 0,
"B", 10, 5,
)
data
|
1
2
3
4
5
6
7
8
9
|
## # A tibble: 6 x 3
## class_name x y
## <chr> <dbl> <dbl>
## 1 A 0 1
## 2 A 10 11
## 3 A 10 21
## 4 B 0 0
## 5 B 10 0
## 6 B 10 5
|
1
2
3
4
|
data %>%
ggplot(aes(x, y, color = class_name)) +
geom_point() +
stat_smooth(formula = y ~ x, method = lm, se = FALSE)
|
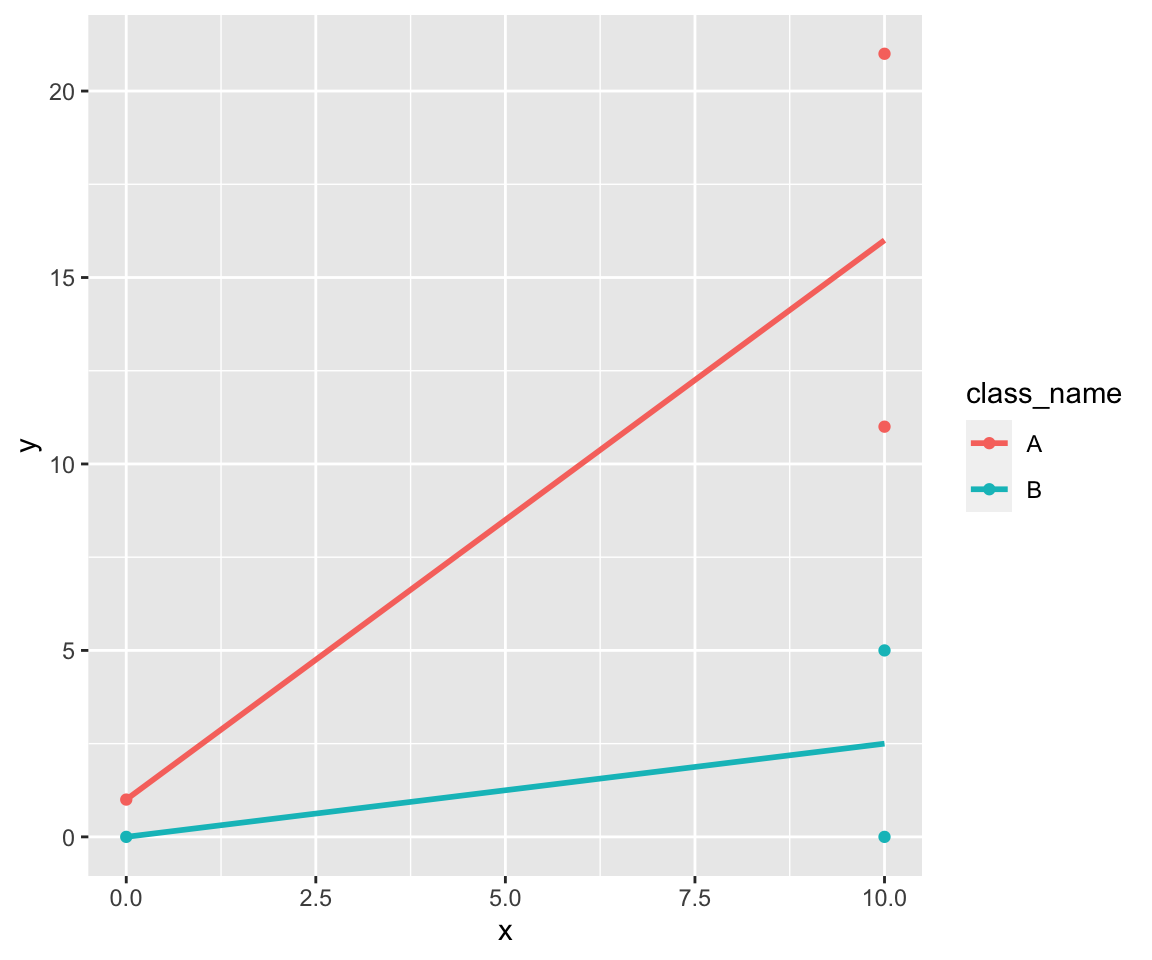
So we’ve only two groups. The linear model is simple:
1
|
lm(y ~ class_name * x, data) %>% summary()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
##
## Call:
## lm(formula = y ~ class_name * x, data = data)
##
## Residuals:
## 1 2 3 4 5 6
## -4.441e-16 -5.000e+00 5.000e+00 1.648e-15 -2.500e+00 2.500e+00
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.0000 5.5902 0.179 0.875
## class_nameB -1.0000 7.9057 -0.126 0.911
## x 1.5000 0.6847 2.191 0.160
## class_nameB:x -1.2500 0.9682 -1.291 0.326
##
## Residual standard error: 5.59 on 2 degrees of freedom
## Multiple R-squared: 0.8201, Adjusted R-squared: 0.5501
## F-statistic: 3.038 on 3 and 2 DF, p-value: 0.2574
|
Step by Step computation
But how can we compute the linear model step by step?
The data
First let’s split the data into $ y $ and $ X $:
1
2
3
4
5
6
7
8
9
10
11
12
|
y <- data %>% pull(y)
X <- data %>%
mutate(
x0 = 1,
x1 = class_name != "A",
x2 = x,
x3 = x1*x
) %>%
select(x0, x1, x2, x3) %>%
as.matrix()
X
|
1
2
3
4
5
6
7
|
## x0 x1 x2 x3
## [1,] 1 0 0 0
## [2,] 1 0 10 0
## [3,] 1 0 10 0
## [4,] 1 1 0 0
## [5,] 1 1 10 10
## [6,] 1 1 10 10
|
So $ y $ contains the values of the dependent variable. $ X $ is a matrix with
$ 1 $ in the first column called $ x_0 $. $ x_1 .. x_3 $ are the predictors.
$ x_3 $ is the interaction between $ x_1 $ and $ x_2 $.
The model
Now we can write our model as:
$$
y = X \beta + \epsilon
$$
We’re searching for $ b $ so that $ \hat{y} = X b $ is the
prediction which minimizes the sum of the squared residuals.
We get $ b $ as
$$
b = (X^t X)^{-1} X^t y
$$
So let’s compute it: (solve computes the inverse of a matrix)
1
2
3
4
|
Xt <- t(X)
b <- solve(Xt %*% X) %*% Xt %*% y
round(b, 3)
|
1
2
3
4
5
|
## [,1]
## x0 1.00
## x1 -1.00
## x2 1.50
## x3 -1.25
|
Standard Errors of the coefficients
Now we’re looking at the standard errors of the coefficients:
We can compute them by
$$
Cov(b) = \sigma^2 (X^t X)^{-1}
$$
A predictior for $ \sigma^2 $ is the mean squared error:
$$
s^2 = \frac{\sum{(y_i - \hat{y})^2}}{df}
$$
In our case the degrees of freedom are $ df = n - 4 $.
1
2
3
4
|
yh <- X %*% b
df <- length(y) - 4
MSE <- sum((y - yh)**2) / df
MSE
|
So the standard errors of the coefficients are the main diagonal of this matrix:
1
|
(solve(Xt %*% X) * MSE) %>% sqrt()
|
1
|
## Warning in sqrt(.): NaNs produced
|
1
2
3
4
5
|
## x0 x1 x2 x3
## x0 5.590170 NaN NaN 1.7677670
## x1 NaN 7.905694 1.7677670 NaN
## x2 NaN 1.767767 0.6846532 NaN
## x3 1.767767 NaN NaN 0.9682458
|
These are the same as computed by lm:
1
|
lm(y ~ class_name * x, data) %>% summary()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
##
## Call:
## lm(formula = y ~ class_name * x, data = data)
##
## Residuals:
## 1 2 3 4 5 6
## -4.441e-16 -5.000e+00 5.000e+00 1.648e-15 -2.500e+00 2.500e+00
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.0000 5.5902 0.179 0.875
## class_nameB -1.0000 7.9057 -0.126 0.911
## x 1.5000 0.6847 2.191 0.160
## class_nameB:x -1.2500 0.9682 -1.291 0.326
##
## Residual standard error: 5.59 on 2 degrees of freedom
## Multiple R-squared: 0.8201, Adjusted R-squared: 0.5501
## F-statistic: 3.038 on 3 and 2 DF, p-value: 0.2574
|
As you can see the covariance matrix isn’t diagnal. Points from “the other group”
also effect the standard error.
So the errors are different to the errors of two independent models:
1
2
3
|
data %>%
group_by(class_name) %>%
group_map(~ coef(summary(lm(y ~ x, data = .x))))
|
1
2
3
4
5
6
7
8
9
|
## [[1]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.0 7.0710678 0.1414214 0.9105615
## x 1.5 0.8660254 1.7320508 0.3333333
##
## [[2]]
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.56395e-16 3.5355339 7.251946e-17 1.0000000
## x 2.50000e-01 0.4330127 5.773503e-01 0.6666667
|
Separate Models
For completeness let’s check the manual way for one single model here:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
data_single <-data %>%
filter(class_name == "A")
y <- data_single %>% pull(y)
X <- data_single %>%
mutate(
x0 = 1,
x1 = class_name != "A",
x2 = x,
x3 = x1*x
) %>%
select(x0, x2) %>%
as.matrix()
X
|
1
2
3
4
|
## x0 x2
## [1,] 1 0
## [2,] 1 10
## [3,] 1 10
|
1
2
3
4
|
Xt <- t(X)
b <- solve(Xt %*% X) %*% Xt %*% y
round(b, 3)
|
1
2
3
|
## [,1]
## x0 1.0
## x2 1.5
|
1
2
3
4
|
yh <- X %*% b
df <- length(y) - 2
MSE <- sum((y - yh)**2) / df
MSE
|
1
|
(solve(Xt %*% X) * MSE) %>% sqrt()
|
1
|
## Warning in sqrt(.): NaNs produced
|
1
2
3
|
## x0 x2
## x0 7.071068 NaN
## x2 NaN 0.8660254
|
Further reading
For more information about multilinear regression look at

